|
This sequence of blog posts will build up into a complete
description of a 2D marine processing sequence and how it is derived.
No processing sequence is definitive and techniques vary with
time (and software), however the idea is to provide a practical guide for
applying seismic processing theory.
The seismic line used is TRV-434 from the Taranaki Basin
offshore New Zealand. It is the same marine line used in our basic tutorial
dataset.
The data are available from New Zealand Petroleum and
Minerals, under the Ministry of Economic Development under the “Open File”
System.
|
The processing sequence developed so far:
|
We need to address and remove linear noise from the shot
record; specifically the direct and refracted arrivals. If these are strong
events, there can be reverberated “copies” (i.e. multiples) that can also cause
problems and need to be removed.
There are three basic approaches we can take for this:
- we can remove the direct and refracted arrivals by applying a front mute to the data; zeroing all of the samples above an event that we pick
- we can try to isolate the linear events in the FK domain and then remove them
- we can try to isolate the linear events in the Tau-P domain and then remove them
Using a mute to remove the direct and refracted arrivals is by
far the easiest method.
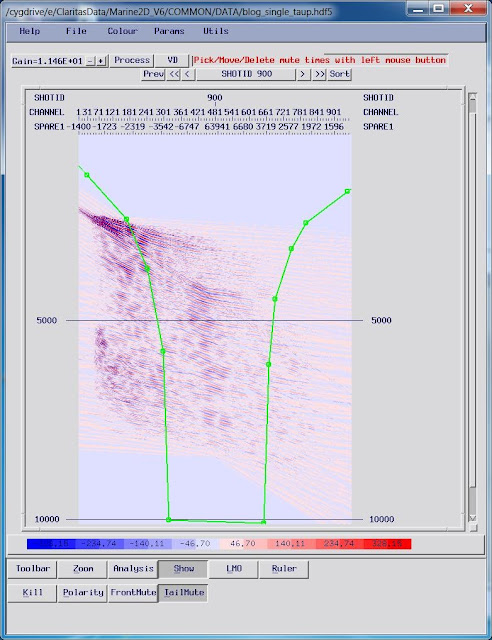
Here’s
an example of how you might pick the front mute on a shot at the start of the
line:
 |
| A typical "front mute" for removal of the direct and refracted arrival. Data above the blue line will be zeroed. |
There are a few tricks to picking the mute, especially in
shallow water.
The first thing to remember is that the mute will need to
have a taper applied; depending on your
software this may start at the time you have picked, end at that time, or be
centred on that time.
The taper is needed to “soften” the boundary from the “hard”
zeros to the actual data. Without the taper we could “clip” waveforms
introducing artificially high frequencies to the dataset leading to artefacts
when we apply further processing.
I’ve also picked the mute to avoid the few inner traces.
This is important in order to preserve the sea-floor event, but it can be
difficult to identify on shallow water datasets. Even if you can spot the
event, the taper can suppress the amplitudes of this event depending on how it
is applied.
We
need to keep at least two traces on our shot gathers, because when we sort from
120-fold shots to 60-fold CDPs, the near channel (120) is only going to be the
near trace in half of the CDPs – in the other half it will be the
second-nearest channel (119).
At this stage it’s important not to be too harsh or
aggressive with the mute – we can always tidy things up later but once you have
removed data, you can’t get it back without re-running.
You need to step through the data checking the refraction
mute you have picked is valid, adding in more control points where needed to
spatially vary the mute with the geology. This is especially important if the
water depth varies.
The problem with a mute is that it limits the information
from the far offsets. Reflection energy is present in the far offsets and we
can use it for picking velocities, imaging and AVO work, but we can’t see it
under all that noise!
The next two approaches are based on linear dips either in
the 2D fourier
transform (FK) domain or the linear Tau-P domain.
Here
are two shot records, from the start and end of the line, plotted out with
their FK response
underneath:
The biggest issue in removing this dipping energy is spatial
aliasing. Spatial aliasing takes place when the apparent, linear dip of an
event is so steep that it is impossible to tell from frequency and wavenumber
alone, which way the event is dipping.
For example, consider a 31 Hz sine wave signal; this has a time
period of (1/31) = 32.25 ms.
Below
are three examples of a 31 Hz sign wave. In the first panel they are unshifted, the
second panel has a 10 ms/trace shift applied, and the third panel has a
17 ms/trace shift applied.
On the second panel the dip direction can be clearly seen as
upper-left to lower-right, but on the third panel (where we have shifted by
approximately half the time period) it is hard to discern the dip direction - it
could also be lower left-to-upper right.
This is an example of spatial aliasing, and shows its
relationship with frequency. With 25m between traces, 17ms/trace corresponds to
25/17=1.470m/ms, or 1470ms-1, which is approximately the speed of
sound in water.
In other words, with a 25m spacing between channels, the
linear direct arrival with an apparent velocity of around 1500ms-1
will be spatially aliased over 31Hz or so, which is exactly what we see on the
shot records.
Spatially aliased linear noise – especially of things like
the tail end of diffractions – is one of the significant causes of apparently
“random” noise – if we can address this we will end up with a much cleaner
section with improved signal strength.
If
we only address the non-aliased part of the direct arrival with an FK domain mute,
we get something like this on SP 900.
While the spatially aliased component is an issue, this
approach has cleaned up a lot of the reverberating linear noise trains below
the first set of refracted arrivals which couldn’t be touched by the front
mute.
To get around the aliasing issue we can design a more
complex mute shape in the FK domain, we still have some reflection energy around
the K=0 axis at 50 Hz or so, which is going to be contaminated by the spatially
aliased direct arrival.
Of course, one answer is to have a smaller trace spacing; if
we had a spacing of 6.25 m, then (approximately) 1500 m/s water bottom arrival
would have dip of 6.25/1500 = 4.16 ms/trace.
This in turn means that only data with a time period less than 8.32 ms
would be aliased, or about 120 Hz.
Some modern data is acquired with this trace spacing, which
is a great help in addressing this issue.
 |
| The FK transform of SP 900 after the data has been interpolated from 25 m group interval (receiver spacing) to 6.25 m to unwrap the spatial aliasing of the direct and refracted arrivals |
The interpolation scheme here is relatively fast to run – it
is a simple polynomial fit to the amplitudes at each time value, with an NMO
applied to remove aliasing - and so
leaves a residual aliased arrival, but critically this crosses the K=0 line at
a much higher frequency (80 Hz+) at the top of the range we are expecting. We
can design an FK domain mute to preserve the reflections and reject the linear
noise much more effectively.
The interpolated FK domain route is a lot more effective
than simply applying an FK mute on the interpolated channels, and offers more
advantages over the basic X-T domain front mute as linear noise throughout the
shot record is also addressed.
The final approach to compare is the Tau-P domain muting
(also termed “linear RADON”); we face the same spatial aliasing issues in the
Tau-P domain as we did with the FK, so again interpolating the data to remove
these will make a big difference.
Using high P-value counts than input data can help to remove
aliasing issues, and so in this case I have used 960 P-values from a
480-channel shot. I’ve also displayed the linear velocities over the transform,
in this case I used -1400ms-1 to 1400ms-1 to cover both
positive and negative dips. The refractions and direct arrivals have negative
dips because channel 1 is the far offset (this may be software dependent). The
channel number is now the “P trace number” and the times have been padded as
part of the Tau-P transform.
 |
| SP 900 with no muting applied (left), FK domain muting (centre) and Tau-P domain muting (right) to address linear noise such as direct and refracted arrivals. In both cases the data has first been interpolated to a 6.25 m interval, and had an “AGC wrap” applied |
When we apply the FK or Tau-P approaches we may also remove
the seafloor event as the water depth is so shallow; it’s usually possible to
avoid this by having a “start time” for the muting process.
In practice the choice of which approach to apply depends on
the a number of factors, including the time you have available to test and
apply different approaches, as the computation time of different transforms can
be significant. The approach I have suggested is quite CPU heavy – to the
extent you’d need to run it in parallel – and so key tests can be whether a
smaller level of interpolation or fewer P-values can get the same results on
your data.
You should check the results from each approach on shot
records from the whole line, as well as stacks.
Other processes are also relevant – if you took the FK
approach to removing swell noise you could combine this with an
interpolation and FK-domain mute to address the direct/refracted arrivals and
save computation time. Similarly we may need to use the Tau-P domain for
deconvolution and can apply that transform only once, which saves processing
time.
In this case, I’ve selected the Tau-P domain result to move
forward with because of the improvement on the low frequencies (and the chance
we’ll use it later on), even though it is expensive computationally.