Marine Processing - Part 5 | Direct Arrivals, Refractions, and Linear Noise

This sequence of blog posts will build up into a complete description of a 2D marine processing sequence and how it is derived.   No processing sequence is definitive and techniques vary with time (and software), however the idea is to provide a practical guide for applying seismic processing theory. The seismic line used is TRV-434 from the Taranaki Basin offshore New Zealand. It is the same marine line used in our basic tutorial dataset. The data are available from New Zealand Petroleum and Minerals, under the Ministry of Economic Development under the “Open File” System.

The processing sequence developed so far: Resample and Minimum Phase Conversion    Reformat from field data (in this case, SEGY) Apply a combined minimum-phase conversion and anti-alias filter Resample to a 4ms sample interval QC and Assign Geometry Assign 2D marine geometry; 12.5m CDP spacing and 60 fold gathers QC shots and near trace plots Amplitude Recovery Amplitude recovery using a T2 Spherical divergence correction Amplitude QC and Edit using peak and RMS amplitude displays Swell Noise Suppression Swell noise suppression using projective filtering

We need to address and remove linear noise from the shot record; specifically the direct and refracted arrivals. If these are strong events, there can be reverberated “copies” (i.e. multiples) that can also cause problems and need to be removed.

There are three basic approaches we can take for this:

• we can remove the direct and refracted arrivals by applying a front mute to the data; zeroing all of the samples above an event that we pick
• we can try to isolate the linear events in the FK domain and then remove them
• we can try to isolate the linear events in the Tau-P domain and then remove them

Using a mute to remove the direct and refracted arrivals is by far the easiest method.

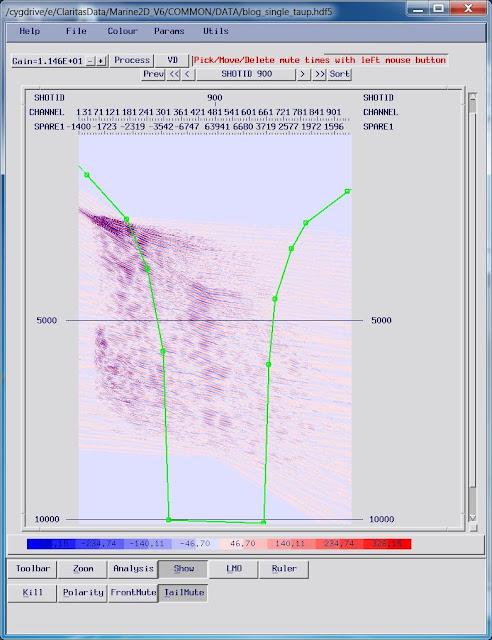
Here’s an example of how you might pick the front mute on a shot at the start of the line:

A typical "front mute" for removal of the direct and refracted arrival. Data above the blue line will be zeroed.

There are a few tricks to picking the mute, especially in shallow water. 

The first thing to remember is that the mute will need to have a taper applied;  depending on your software this may start at the time you have picked, end at that time, or be centred on that time.

The taper is needed to “soften” the boundary from the “hard” zeros to the actual data. Without the taper we could “clip” waveforms introducing artificially high frequencies to the dataset leading to artefacts when we apply further processing.

I’ve also picked the mute to avoid the few inner traces. This is important in order to preserve the sea-floor event, but it can be difficult to identify on shallow water datasets. Even if you can spot the event, the taper can suppress the amplitudes of this event depending on how it is applied. 

We need to keep at least two traces on our shot gathers, because when we sort from 120-fold shots to 60-fold CDPs, the near channel (120) is only going to be the near trace in half of the CDPs – in the other half it will be the second-nearest channel (119).

At this stage it’s important not to be too harsh or aggressive with the mute – we can always tidy things up later but once you have removed data, you can’t get it back without re-running.

You need to step through the data checking the refraction mute you have picked is valid, adding in more control points where needed to spatially vary the mute with the geology. This is especially important if the water depth varies.

The problem with a mute is that it limits the information from the far offsets. Reflection energy is present in the far offsets and we can use it for picking velocities, imaging and AVO work, but we can’t see it under all that noise!

The next two approaches are based on linear dips either in the 2D fourier transform (FK) domain or the linear Tau-P domain.  

Here are two shot records, from the start and end of the line, plotted out with their FK response underneath:

The FK response of two shot records (which have had gain recovery and swell-noise supression applied). The linear direct and refracted arrivals we want to remove map into the marked out areas. Above about 31 Hz the signal becomes spatially aliased. Note the additional linear noise on SP 800 throughout the record, caused by multiples of the refracted arrivals

The biggest issue in removing this dipping energy is spatial aliasing. Spatial aliasing takes place when the apparent, linear dip of an event is so steep that it is impossible to tell from frequency and wavenumber alone, which way the event is dipping.

 

For example, consider a 31 Hz sine wave signal; this has a time period of (1/31) = 32.25 ms.

Below are three examples of a 31 Hz sign wave. In the first panel they are unshifted, the second panel has a 10 ms/trace shift applied, and the third panel has a 17 ms/trace shift applied.

Three panels showing 20 traces with a 31 Hz sine wave. The first panel has no shifts applied, the second has a 10ms/trace shifts and the third has 17ms/trace shifts. The dip direction is obvious on the second panel, but ambiguous on the third panel – the data are spatially aliased

On the second panel the dip direction can be clearly seen as upper-left to lower-right, but on the third panel (where we have shifted by approximately half the time period) it is hard to discern the dip direction - it could also be lower left-to-upper right.

This is an example of spatial aliasing, and shows its relationship with frequency. With 25m between traces, 17ms/trace corresponds to 25/17=1.470m/ms, or 1470ms^-1, which is approximately the speed of sound in water.

In other words, with a 25m spacing between channels, the linear direct arrival with an apparent velocity of around 1500ms^-1 will be spatially aliased over 31Hz or so, which is exactly what we see on the shot records.

  

Spatially aliased linear noise – especially of things like the tail end of diffractions – is one of the significant causes of apparently “random” noise – if we can address this we will end up with a much cleaner section with improved signal strength.

If we only address the non-aliased part of the direct arrival with an FK domain mute, we get something like this on SP 900.

Impact of using an FK domain mute on SP 900 to remove the non-aliased part of the direct and refracted arrivals only. Above is the FK domain display, and below the shot record before (left) and after (right) the FK domain mute. The spatially aliased energy is characterised by a “reverse dipping chevron” effect, and still contaminates the data

While the spatially aliased component is an issue, this approach has cleaned up a lot of the reverberating linear noise trains below the first set of refracted arrivals which couldn’t be touched by the front mute.

 

To get around the aliasing issue we can design a more complex mute shape in the FK domain, we still have some reflection energy around the K=0 axis at 50 Hz or so, which is going to be contaminated by the spatially aliased direct arrival.

Of course, one answer is to have a smaller trace spacing; if we had a spacing of 6.25 m, then (approximately) 1500 m/s water bottom arrival would have dip of 6.25/1500 = 4.16 ms/trace.  This in turn means that only data with a time period less than 8.32 ms would be aliased, or about 120 Hz.

Some modern data is acquired with this trace spacing, which is a great help in addressing this issue.

We can try and simulate this by interpolating the data from a 25 m channel interval up to a 6.25 m interval, and then using an appropriate FK domain mute, ideally with an “AGC wrap” to avoid amplitude issues.

The FK transform of SP 900 after the data has been interpolated from 25 m group interval (receiver spacing) to 6.25 m to unwrap the spatial aliasing of the direct and refracted arrivals

The interpolation scheme here is relatively fast to run – it is a simple polynomial fit to the amplitudes at each time value, with an NMO applied to remove aliasing - and so leaves a residual aliased arrival, but critically this crosses the K=0 line at a much higher frequency (80 Hz+) at the top of the range we are expecting. We can design an FK domain mute to preserve the reflections and reject the linear noise much more effectively.

Comparing the FK results we get this:

SP 900, with no FK muting (left), FK muting with 25 m trace spacing (centre) and FK muting applied with interpolation to 6.25 m trace spacing (right); the dipping noise can be removed from the shot record more effectively with interpolation

The interpolated FK domain route is a lot more effective than simply applying an FK mute on the interpolated channels, and offers more advantages over the basic X-T domain front mute as linear noise throughout the shot record is also addressed.

The final approach to compare is the Tau-P domain muting (also termed “linear RADON”); we face the same spatial aliasing issues in the Tau-P domain as we did with the FK, so again interpolating the data to remove these will make a big difference.

In the Tau-P domain we can vary what linear dips we want to remove with the time (Tau) value, giving a lot more control than the FK domain.

Tau-P transform of SP 900, with an interpolation to 6.25 m trace spacing applied first. 960 P values have been used, with the traces labelled by their linear velocity. The transform includes both negative and positive dips (remembering channel 1 is the far offset) ; a “tail mute” has been picked to isolate the reflection data (higher apparent velocities) from the linear noise (lower values) 

Using high P-value counts than input data can help to remove aliasing issues, and so in this case I have used 960 P-values from a 480-channel shot. I’ve also displayed the linear velocities over the transform, in this case I used -1400ms^-1 to 1400ms^-1 to cover both positive and negative dips. The refractions and direct arrivals have negative dips because channel 1 is the far offset (this may be software dependent). The channel number is now the “P trace number” and the times have been padded as part of the Tau-P transform.

To attack the linear noise, I have designed a “tail mute” (green line) below which the data will be zeroed. As with other mutes (FK or XT), there will be a taper applied to the data which needs to be taken into account in the mute design.

SP 900 with no muting applied (left), FK domain muting (centre) and Tau-P domain muting (right) to address linear noise such as direct and refracted arrivals. In both cases the data has first been interpolated to a 6.25 m interval, and had an “AGC wrap” applied

When we apply the FK or Tau-P approaches we may also remove the seafloor event as the water depth is so shallow; it’s usually possible to avoid this by having a “start time” for the muting process.

In practice the choice of which approach to apply depends on the a number of factors, including the time you have available to test and apply different approaches, as the computation time of different transforms can be significant. The approach I have suggested is quite CPU heavy – to the extent you’d need to run it in parallel – and so key tests can be whether a smaller level of interpolation or fewer P-values can get the same results on your data.

You should check the results from each approach on shot records from the whole line, as well as stacks.

Other processes are also relevant – if you took the FK approach to removing swell noise you could combine this with an interpolation and FK-domain mute to address the direct/refracted arrivals and save computation time. Similarly we may need to use the Tau-P domain for deconvolution and can apply that transform only once, which saves processing time.

In this case, I’ve selected the Tau-P domain result to move forward with because of the improvement on the low frequencies (and the chance we’ll use it later on), even though it is expensive computationally.

To see the impact of the processing so far, it is also important to compare the stacked sections.

Stacked sections: Brute Stack (Spherical Divergence only) and the current stack, with additional swell noise removal and Tau-P domain linear noise removal. The stacks have a constant velocity and fixed-percentage stretch mute applied. Note the impact of removing the steep-dip noise on the deeper section

By: Guy Maslen